L-system based fractals and graphics

Experiments with generating L-system based fractal graphics using numpy and maplotlib. Managed to create the famous Koch snowflake and dragon curve dragon curve as well, along with some interesting looking pictures, and some likely candidates for a fractal tiling of the plane.

Python implementation

First, let’s define the steps in a simple way. The way to create these graphics is as follows:

1. Create a fractal ‘word’
   1. Define an ‘alphabet’: This is the possible values of the letters in a ‘word’
   2. Define a set of ‘substitution rules’: For each letter in the alphabet, create a mapping to what it should be substituted for
   3. Define a ‘seed word’: A starting point for the word
   4. Iteratively substitute each letter in the word using the substitution rules till a certain depth
2. Create a graphic from the created word
   1. For each letter in the alphabet, assign a vector.
   2. Take the formed word and map each letter to its corresponding vector
   3. Plot that series of vectors end to end on the xy plane

In the below system, for prettiness, all letters are assigned to vectors at uniform angles to complete 360 degrees. For example, an alphabet with 4 letters will be mapped to 4 vectors along the +- x-y axes. Four functions are defined below.

1. circ_cart_unit: Helper function, returns (x,y) coordinates along the unit circle given an angle
2. gen_reg_alphabet: Generates an alphabet of uniformly angled vectors given a size of the alphabet. Components of alphabet will be list of x,y coordinates of vectors. Alphabets will be referred to by their indices in this list.
3. substitute_rec: Recursive function to create word as per substitution rules (subs_map) and seed (start_list). Subs_map is a dictionary which maps letters (represented by integers = indices in the alphabet) to what they should be substituted by. This will run for a given number of iterations.
4. plot_vect_list: Given a generated ‘word’, i.e. list of letters (= integers = indices) plot them as per the alphabet vectors end to end. First letter will start from the origin, second will start from the end of the first and so on.

def circ_cart_unit(theta):
    """
    Return x, y coordinates on the unit circle from a given angle
    """
    return [np.cos(theta),np.sin(theta)]

def gen_reg_alphabet(size):
    """
    Create an 'alphabet' for the substitution rule and assign vectors at uniform angles 
    """
    alphabet = []
    for i in range(size):
        alphabet.append(circ_cart_unit(2*np.pi*(i/size)))
        
    return alphabet

def substitute_rec(start_list,subs_map,iterations):
    """
    Recursive function to create word as per substitution rules (subs_map) and seed (start_list)
    """
    if iterations==1:
        return np.array([subs_map[n] for n in start_list]).flatten()
    else:
        return substitute_rec(np.array([subs_map[n] for n in start_list]).flatten(),subs_map,iterations-1)

def plot_vect_list(alph_array,alphabet,color='tab:blue',ax=None):
    """
    Given a word (alph_array) and a mapping (alphabet), plot it
    """
    vec_array = np.array([alphabet[k] for k in alph_array])
    plt_test = np.concatenate([np.array([[0,0]]),np.cumsum(vec_array,axis=0)])
    
    
    if not ax:
        fig,ax = plt.subplots(figsize=(12,12))
    ax.plot(plt_test[:,0],plt_test[:,1],color)
    ax.set_aspect('equal', adjustable='box')
    return ax

Creating some art

Koch snowflake

Now let us create some art! Let’s start with 6 letters. The alphabet will be unit vectors at 0, 60, 120, 180, 240 and 300 degree angles.

alphabet_6 = gen_reg_alphabet(6)

To create the Koch snowflake, we’ll need it’s well known substitution rule:

# koch snowflake map
subs_dict_koch = {0:[0,1,5,0],
             1:[1,2,0,1],
             2:[2,3,1,2],
             3:[3,4,2,3],
             4:[4,5,3,4],
             5:[5,0,4,5]
            }

Let’s see how we can plot that using the functions we defined.

koch_sub_array_0 = substitute_rec([0],subs_dict_koch,1) # 1 iteration, starting from [0]
plot_vect_list(koch_sub_array_0,alphabet_6)

koch_sub_array = substitute_rec([0],subs_dict_koch,8) # 8 iterations, starting from [0]
plot_vect_list(koch_sub_array,alphabet_6)

Below is what this substitution rule does to a simple $[0]$ word ((0,0) to (1,0)) in some iterations: 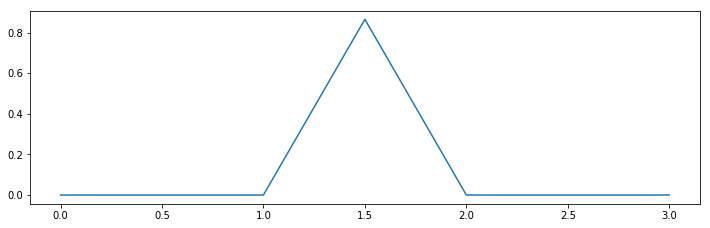Koch Snowflake, 1 step starting from $[0]$ Koch Snowflake, 2 steps starting from $[0]$ Koch Snowflake, 8 steps starting from $[0]$

Now, if we start from a hexagon word ($[0,1,2,3,4,5]$) what does this give us? A snowflake indeed! Koch Snowflake, 5 steps starting from a hexagon

Z-rule

Let’s try substituting each letter with an inverted “Z” shape. For the purposes of this post, let me call this a “z-rule”. The rules will be as follows:

subs_dict_1 = {0:[0,2,0],
               1:[1,3,1],
               2:[2,4,2],
               3:[3,5,3],
               4:[4,0,4],
               5:[5,1,5]
              }

What does this look like?

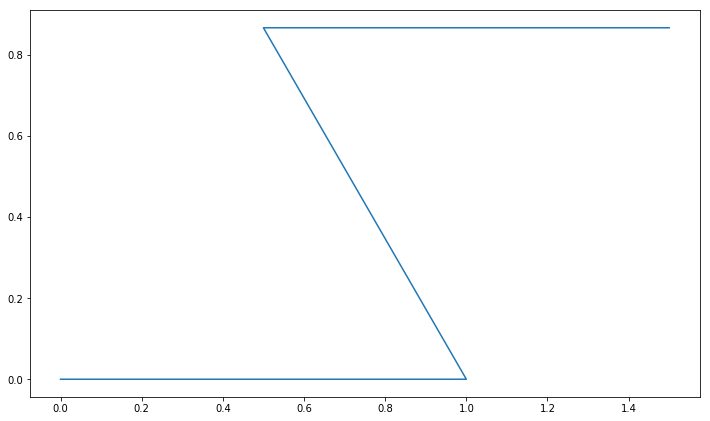Z-rule, 1 step starting from $[0]$ 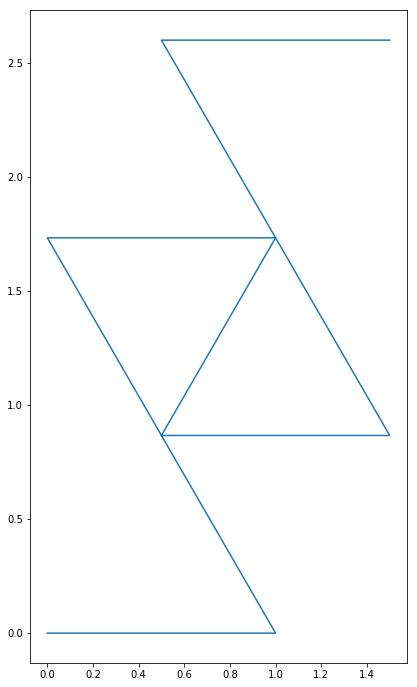Z-rule, 2 steps starting from $[0]$ Z-rule, 8 steps starting from $[0]$ Z-rule, 10 steps starting from $[0]$

Now let’s try starting from a different word, say $[0,2,4]$, a triangle. Z-rule, 9 steps starting from $[0,2,4]$

Half-Hexagon rule

Let’s try another substitution rule. I call this the “half hexagon”. This time I’m defining a set of rules using a pattern, instead of hardcoding it. This should work because the substitution rules have been symmetric (so far!). Assymetric rules should also be possible using patterns, although it would probably be easier to just write it out than work out the pattern.

subs_dict_3 = {i:[(i+1)%6,(i+2)%6,(i+3)%6] for i in range(6)}

Half-hexagon rule, 1 step starting from $[0]$ Half-hexagon rule, 8 steps starting from $[0]$ If we combine two of these together, we get a neat little fractal hexagon. Notice the self-similar shapes inside each side of the hexagon. The almost hexagonal shapes inside them have similar patterns at a smaller scale! If we keep going to infinity these will keep going in a fractal manner.

Half-hexagon rule, 8 steps starting from $[0,3]$

Flat Z-rule

We can flatten the z-rule out, so that it’s an obtuse angled flat z, with the following rules.

subs_dict_4 = {i:[i,(i+1)%6,i] for i in range(6)}

This looks like below: 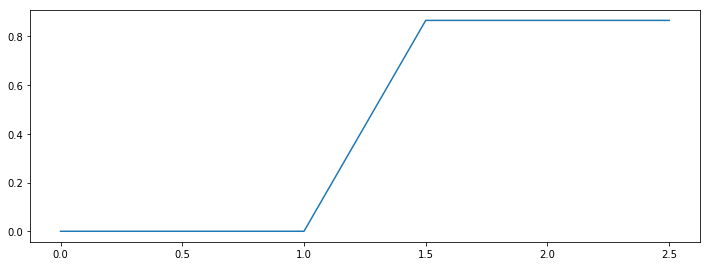Flat Z-rule, 1 step starting from $[0]$

Now let us try a few different patterns on the same plot:

test_4_sub_array_2_1 = substitute_rec([0,1,2,3,4,5],subs_dict_4,5)
test_4_sub_array_2_2 = substitute_rec([2,3,4,5,0,1],subs_dict_4,5)
test_4_sub_array_2_3 = substitute_rec([4,5,0,1,2,3],subs_dict_4,5)
ax = plot_vect_list(test_4_sub_array_2_1,alphabet_6)
ax = plot_vect_list(test_4_sub_array_2_2,alphabet_6,ax=ax,color='tab:orange')
plot_vect_list(test_4_sub_array_2_3,alphabet_6,ax=ax,color='tab:cyan')

This results in a beautiful fractal tiling of the plane. I’m pretty sure this will only be a perfect tiling when taken to infinity, and slightly imperfect at finite steps. 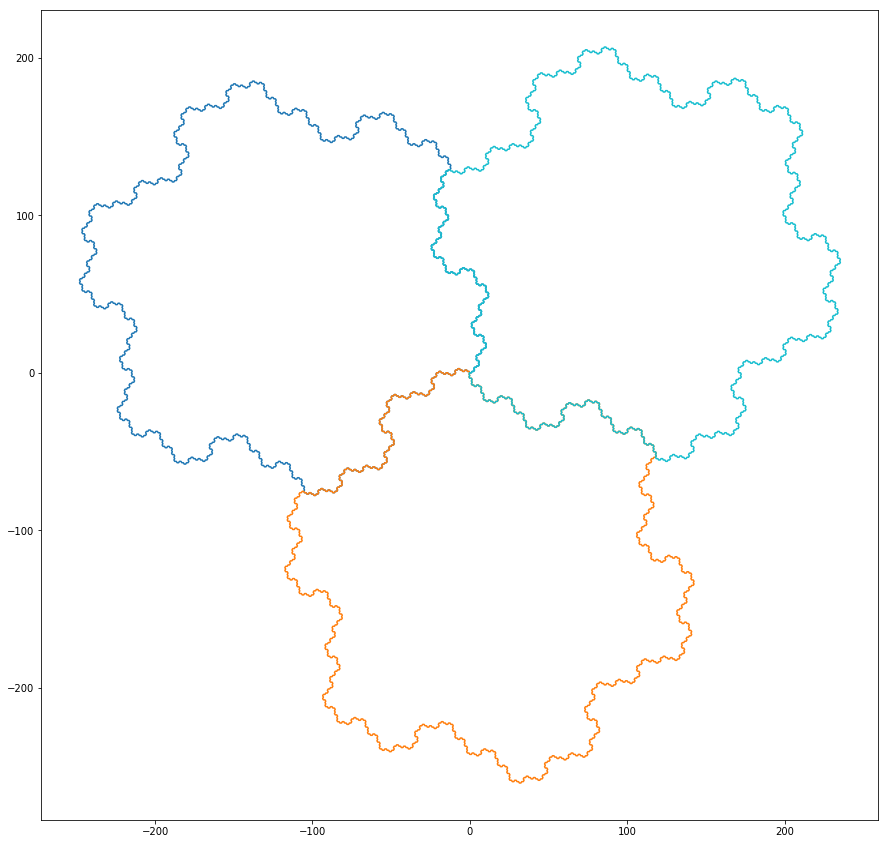Flat Z-rule tiling, 5 steps

Dragon curve

For the dragon curve we need a 4 letter alphabet, which will result in 4 unit vectors at right angles to each other. It can be obtained from the following substitution rule:

subs_dict_4_4 = {0:[0,1],
                 1:[2,1],
                 2:[2,3],
                 3:[0,3]
                }

Dragon curve rule, 13 steps starting from $[0]$

A dragon curve also tiles the plane: Dragon curve tiling, 12 steps

Other interesting pictures

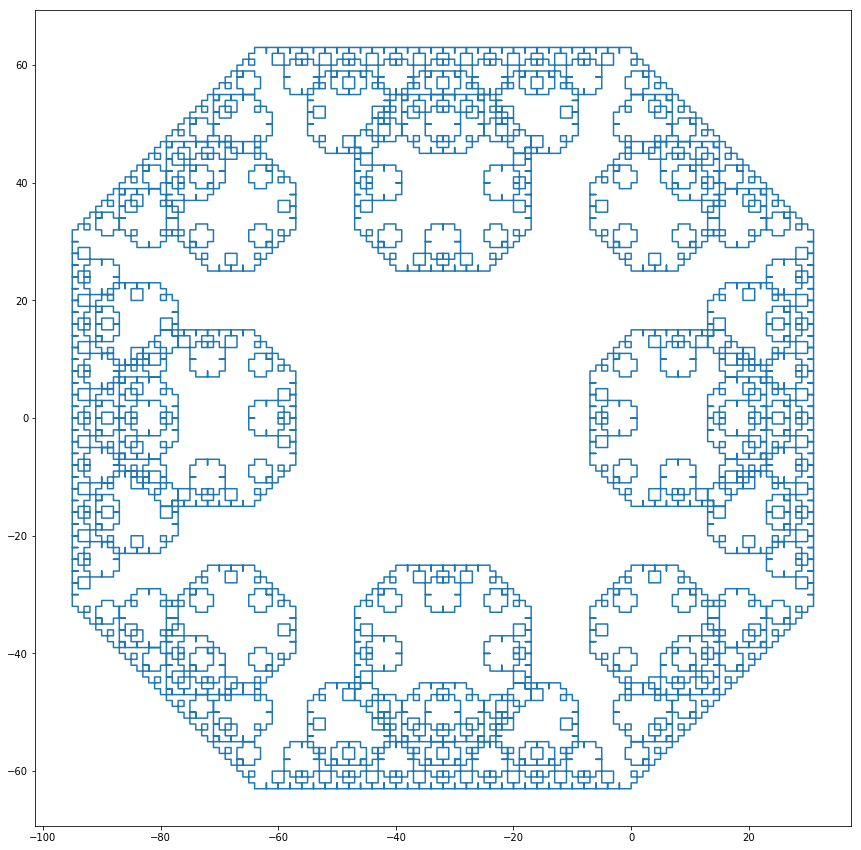8 letter alphabet rule, 12 steps. Looks like a nice pattern to have on a rug

Another 8 letter alphabet rule, 5 steps. Fractal thought bubble

Series of substitutions

A variant on the above concept could be a series of substitutions from a list, applied in sequence. Essentially instead of a single map it will be a list of maps applied in order and repeated as per iterations. The recursive function for this will look as follows:

def substitute_rec_gen(start_list,subs_map_list,iterations):
    if iterations==0:
        return np.array([subs_map_list[0][n] for n in start_list]).flatten()
    else:
        return substitute_rec_gen(np.array([subs_map_list[(iterations-1)%len(subs_map_list)][n] for n in start_list]).flatten(),subs_map_list,iterations-1)

I tried a few designs with a list of two mappings, but unfortunately couldn’t find too many interesting patterns. One slightly intriguing one:

subs_dict_list_4_1 = [{i:[i,(i+1)%4,i] for i in range(4)}, {i:[i,(i-1)%4,(i-2)%4,i] for i in range(4)}]

4 letter alphabet rule set of 2, 6 steps. Fractal swastika